Flowchart Of Dijkstra Algorithm

The distance estimation method is applied to approximate the shortest path by using the above algorithm based on the lane deviation and the estimated straight path.

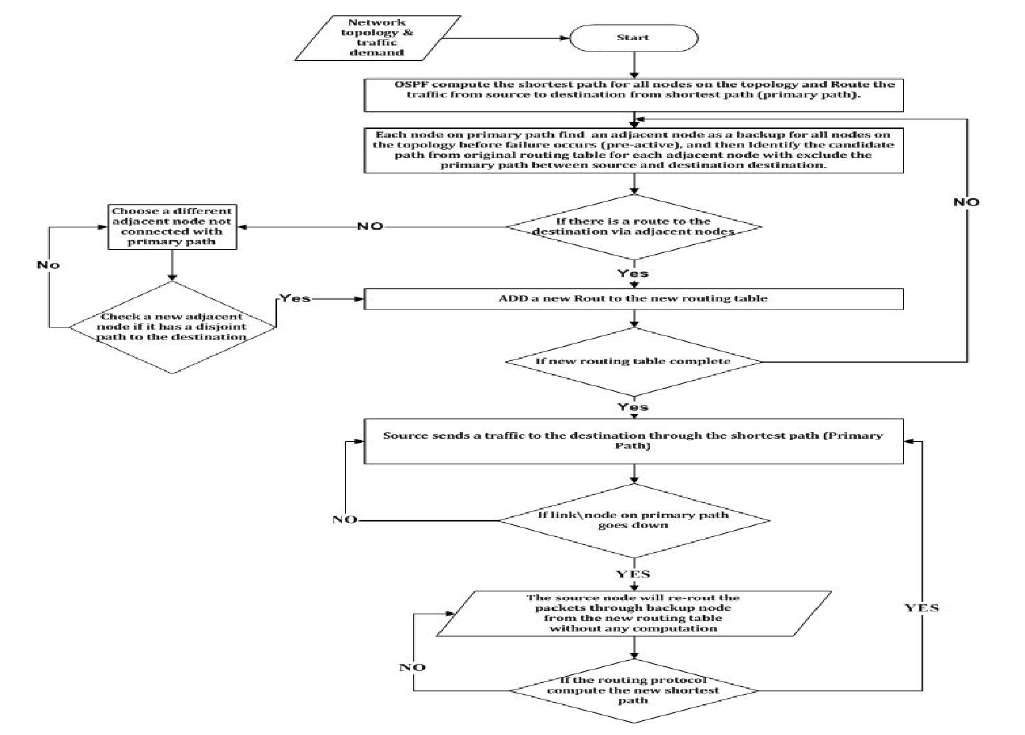
Flowchart of dijkstra algorithm. Given for digraphs but easily modified to work on undirected graphs. The main purpose of a flowchart is to analyze different processes. Using the dijkstra algorithm it is possible to determine the shortest distance or the least effort lowest cost between a start node and any other node in a graph. A flowchart is the graphical or pictorial representation of an algorithm with the help of different symbols shapes and arrows in order to demonstrate a process or a program.

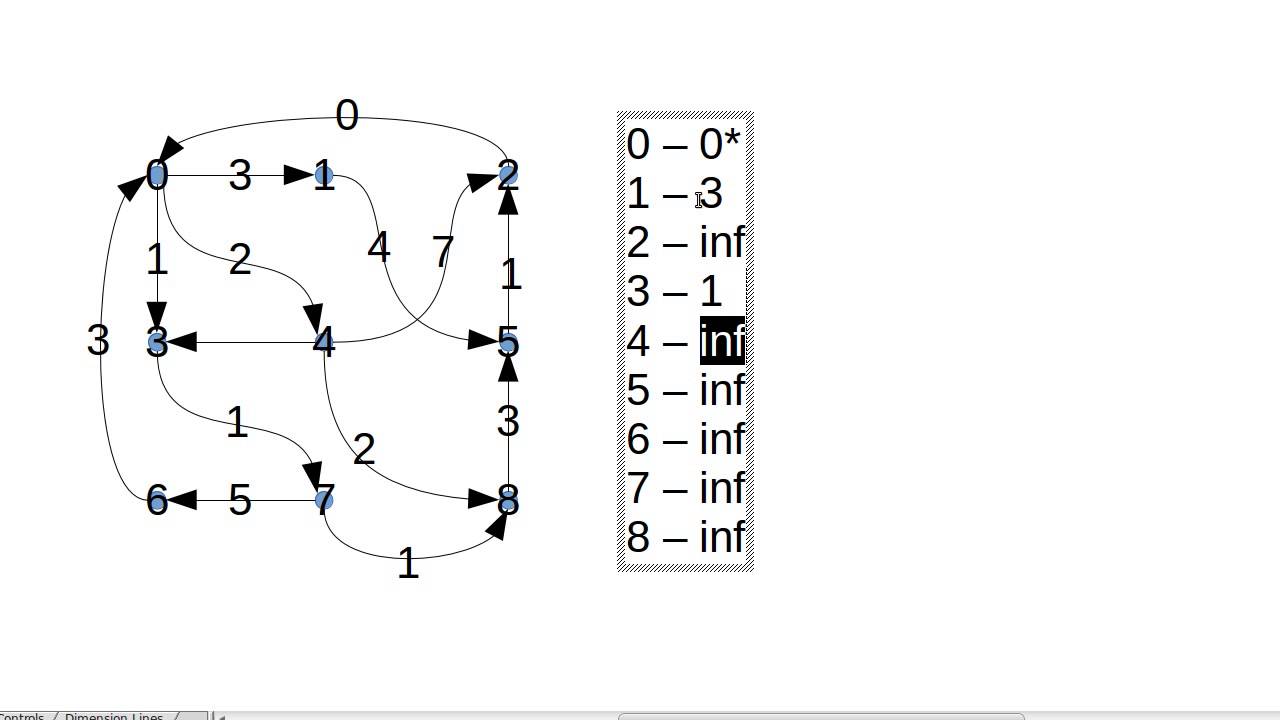
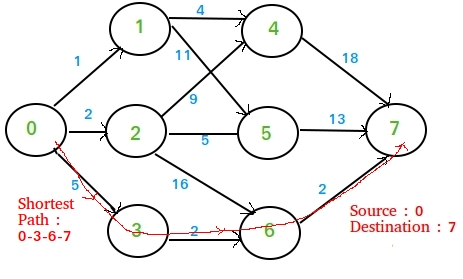
Like prim s mst we generate a spt shortest path tree with given source as root. We maintain two sets one set contains vertices included in shortest path tree other set includes vertices not yet included in shortest path tree. Dijkstra s algorithm is an algorithm for finding the shortest paths between nodes in a graph which may represent for example road networks. The idea of the algorithm is to continiously calculate the shortest distance beginning from a starting point and to exclude longer distances when making an update.

Loops are marked in the image given below. In this tutorial we will learn to find shortest path between two vertices of a graph using dijkstra s algorithm. Dijkstra s algorithm is very similar to prim s algorithm for minimum spanning tree. With algorithms we can easily understand a program.

Any edge that starts and ends at the same vertex is a loop. Dijkstra s algorithm and flow chart with implementation in java. Dijkstra s original algorithm found the shortest path between two given nodes but a more common variant fixes a single node as the source node and finds shortest paths from the source to all other nodes in the graph. Dijkstra s algorithm works on the basis that any subpath b d of the shortest path a d between vertices a and d is also the shortest path between vertices b and d.

The shortest path problem for weighted digraphs. Dijkstra s shortest path algorithm clrs 24 3 outline of this lecture recalling the bfs solution of the shortest path problem for unweighted di graphs. Dijkstra in 1956 and published three years later. Djikstra used this property in the opposite direction i e we overestimate the distance of each vertex from the starting vertex.

On the basis of the experimental results when comparing qof and ctp mechanisms qof outperforms ctp on optimal data delivery path and the faulty node exclusion. E dijkstra s algorithm maintains a set s of vertices whose final shortest the path weights from the source s have already been determined. Consider the following graph. It was conceived by computer scientist edsger w.